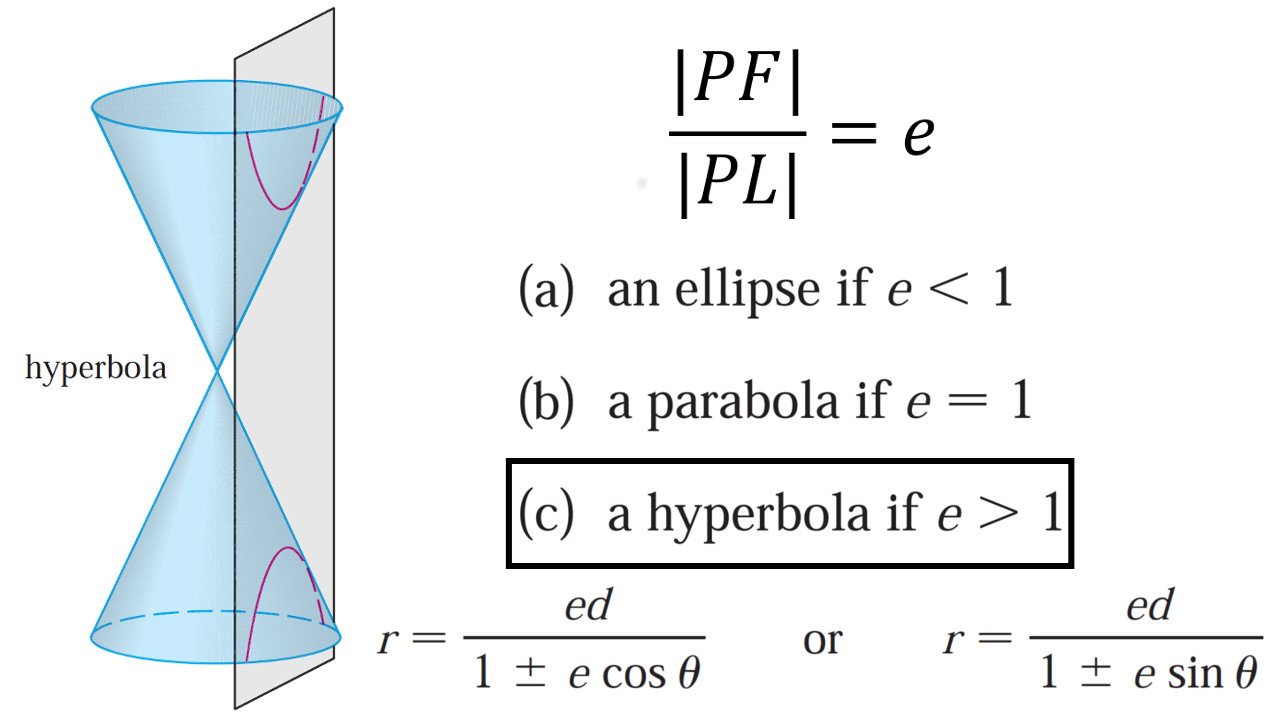
Conics In Polar Form - Identifying a conic in polar form. A single focus, a fixed line called the directrix, and the. Identifying a conic in polar form. Any conic may be determined by three characteristics: Any conic may be determined by three characteristics: Identifying a conic in polar form. Identifying a conic in polar form. A single focus, a fixed line called the directrix, and the. A single focus, a fixed line called the directrix, and the. Each of these orbits can be modeled by a conic section in the polar coordinate system.
Identifying a conic in polar form. A single focus, a fixed line called the directrix, and the. A single focus, a fixed line called the directrix, and the. Conic sections in polar coordinates. Each of these orbits can be modeled by a conic section in the polar coordinate system. Identify a conic in polar form. Any conic may be determined by three characteristics: Identifying a conic in polar form. Identifying a conic in polar form. Identifying a conic given the polar form. For each of the following equations, identify the conic with focus at the origin, the directrix,. Any conic may be determined by three characteristics: A single focus, a fixed line called the directrix, and the. By the end of this section, you will be able to: Identifying a conic in polar form. Any conic may be determined by three characteristics: